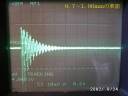
| 太鼓を科学する・その1 自作桶胴太鼓の場合 Return 手元にあった古〜いデジタル・ストレージオシロスコープ(100MHz帯域)に火を入れたらどうにか動いたので、 マイクロフォンを接続して早速自作太鼓の波形を撮ってみました。これでなにか分かるかな〜。 いろいろな太鼓の音を波形で比べてみれば、段々となにかがわかって来るでしょうね。 きっと! 注意:どうも実験に使ったマイクロフォンが飽和しているようです。 つまり太鼓の音が大きすぎて、マイクロフォンの振動膜が追従できないでいるのではないかと思われます。 振動波形の下方向に引っ張られている様に見えるのは、逆に上の方が飽和して、これ以上信号が出せない状態であるようです。 もっと小さな音で実験しなおさないとだめかも知れません。 ただ余韻、周期・周波数等には影響しませんので、そのつもりでご覧下さい。 |
|
| |
|

|
−使用した太鼓のプロフィール−
金輪外寸:1尺5寸、 胴の外寸:1尺3寸、胴長1尺8寸 打面の革:0.7mm〜1.00mmの牛革 (ただし裏面には1〜1.2mmの革が張ってあります) 胴材:14mmの杉板20枚 |
| 太鼓を床から50cmほど浮かして、革の面の中心から30cmのところにマイクロフォンを置き、正面から録音。オシロスコープの画面の上に縦に見える細くて黒い線が0.2秒間隔ですから、面を打った瞬間から、最大値の70%くらいまで波形が減衰するのに約0.4秒かかっています。これが長ければ、「ど〜〜〜〜ん」と伸びのある音になるのでしょうね。 時間軸(横方向) 0.2S/DIV 説明:DIVとはDivisionの略で、オシロスコープの画面の上にある、縦、横の線と線の間のことを言います。 02.S/DIVとは 輝点がある線から次の線に到達するのに0.2秒かかることを意味しています。 |
|
|
上の波形を横方向に拡大しました。 上では滑らかに波形が減衰しているように見えましたが、良く見ると小さな凸凹が沢山ありますね。このあたりが太鼓固有の特徴ある音を形成しているのかも知れませんね。約20サイクルで音が大きくなったり小さくなったりしながら、全体としては0.4〜0.5秒くらいで音が減衰しています。 音のイメージとしては「わんわん わんわん、、、」てな感じでしょうか。
この20サイクルくらいの音のうねりが、太鼓の構造上どこから来るのかが、キイになりそうですね。 時間軸(横方向) 0.1S/DIV |
|
|
・さらに横方向に拡大すると、やっぱりね。 きれいに音がうねっていますので、やはり構造からくる物のようです。サイズを変えたりするとうねりも当然変化するのでしょう。
・予測では、左右の革の厚さの違いから来る共振周波数の差がビートとなって出ているのだと思います。 例えば右の革が100Hzで振動し、左の革が120Hzで共振していると、その差の20Hzがビートとなって現れてきますね。 多分ね〜。 下でも書いてますが、うねりの中にある高い周波数は約100サイクルです。その100サイクルが20サイクルでうねりながら減衰しています。その組み合わせが微妙な音の違いを生むのかな?? 時間軸(横方向) 50mS/DIV |
|
|
★これはやっぱりビートが発生しているように見えます。
今回実験に使ったオシロスコープは、電気信号を画面に波形として表現してくれますが、複数の波形が合成された信号の場合は、分析が難しいです。 これはオシロスコープが時間方向に電気信号の変化を表現しているからなんですね。 で、どの様な周波数の信号がどの程度の量含まれているかを測定するには、やっぱりスペクトラムアナライザーが欲しいですね、、、。 時間軸(横方向) 20mS/DIV |
|
|
もっと拡大します。 大きな波形の頭が大体縦の黒い線に重なっています。 と言う事は、波長が10mSという事ですね。 つまり周波数はその逆数ですから、1/10mS
= 100Hz となり、約100サイクルです。でも結構いろいろな波形が重なっていてあまり綺麗とは言えませんね。専門的には「ハーモニックス」とか「高調波」と呼ばれる、基本の波形の整数倍の周波数の波形が載っているのではないかと思われます。
胴の長手方向、胴の直径方向、革の固有振動数、それらが混ざって複雑な波形になっているのでしょうね。
時間軸(横方向) 10mS/DIV |
|
| |
|
|
■太鼓の胴と革が同じ周波数で共振すると、少ないエネルギーで良い音、大きい音が出ると言われています。
単純な計算ですと、太鼓の面から面までの距離で胴そのものの一番低い共振周波数が求められると思います。といっても、胴の長さが直径より長い場合の話だと思いますが。
共振周波数を "Fc" とし、面と面の距離(胴の長さに同じ)を "L" とし、音速を 340m として計算すると、Fc=340/2L で胴の共振周波数が求められます。 使った太鼓の面と面の距離は53cmですから、計算すると以下の通り: Fc=340/(2x0.53) =320Hz となります。 オシロスコープの波形ですと、概略100Hz とずいぶん低めに出ていますが、この差はなんだろう?? 胴の寸法で決まる共振周波数 革の面積・質量・密度等できまる共振周波数 それらの相互作用で決まる共振周波数、、、きっといろんな要素が関係しているのでしょうね? ある文献によると、上記の式で求められるのは、硬い密閉の場合であって、太鼓のように左右に(上下か?)革が張ってあると、密閉とは言えず、見掛けの胴の長さが長くなったように振舞う、、とのこと。つまり胴が長くなれば、共振周波数は低くなりますね。 で、上の式から、100Hzで共振する周波数を求めると、胴の長さが1.7メートルになります。 つまり、この自作太鼓と同じ周波数で共振させようとするならば、1.7メートルの胴の密閉箱を作れば良いことになるわけですね。。。。 それが分かったからってなんの意味があるの???? う〜〜〜ん、、まあ、太鼓の波形ってあんななんだって思って頂ければ幸いです、、、。 注意:今回の試験に使った太鼓は両面の革の厚さが異なりますので、代表的な太鼓とは言えません。今度は両面ともほぼ同一の革を張った太鼓で試して見ます。 |
|
|
All right reserved (C) 2002 T.Baba
|
|